Let
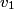 and and 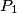 denote the pressure in the constriction. The fluid is incompressible, so denote the pressure in the constriction. The fluid is incompressible, so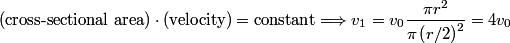 Also, from Bernoulli's equation, we have that 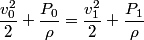 This implies that 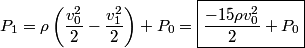 Therefore, answer (A) is correct. |
Let
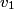 and and 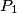 denote the pressure in the constriction. The fluid is incompressible, so denote the pressure in the constriction. The fluid is incompressible, so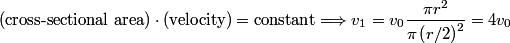 Also, from Bernoulli's equation, we have that 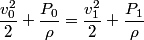 This implies that 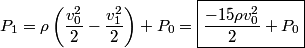 Therefore, answer (A) is correct. |